Pythagorova věta

Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků. Umožňuje dopočítat délku třetí strany takového trojúhelníku, pokud jsou známy délky dvou zbývajících stran.

Pythagorovu větu můžeš použít pouze u pravoúhlého trojúhelníku. V žádném jiném typu trojúhelníku nefunguje.

Pokud jsou a,b odvěsny a c je přepona, pak platí: \(c^2=a^2+b^2\). Z tohoto vzorce vypočítáš přeponu. Budeš-li počítat odvěsnu a, pak použiješ tuto podobu Pythagorovy věty: \(a^2=c^2-b^2\). Budeš-li počítat odvěsnu b, pak použiješ tuto podobu Pythagorovy věty: \(b^2=c^2-a^2\).

Pamatuj, že prostě vždy „nejdelší strana na druhou je rovna první odvěsna na druhou plus druhá odvěsna na druhou“. Někdy tě totiž může při použití Pythagorovy věty splést to, že přepona se nebude jmenovat c, ale bude to a a ty budeš muset použít Pythagorovu větu takto: \(a^2=b^2+c^2\), abys počítal/a správně.

Praktický výpočet

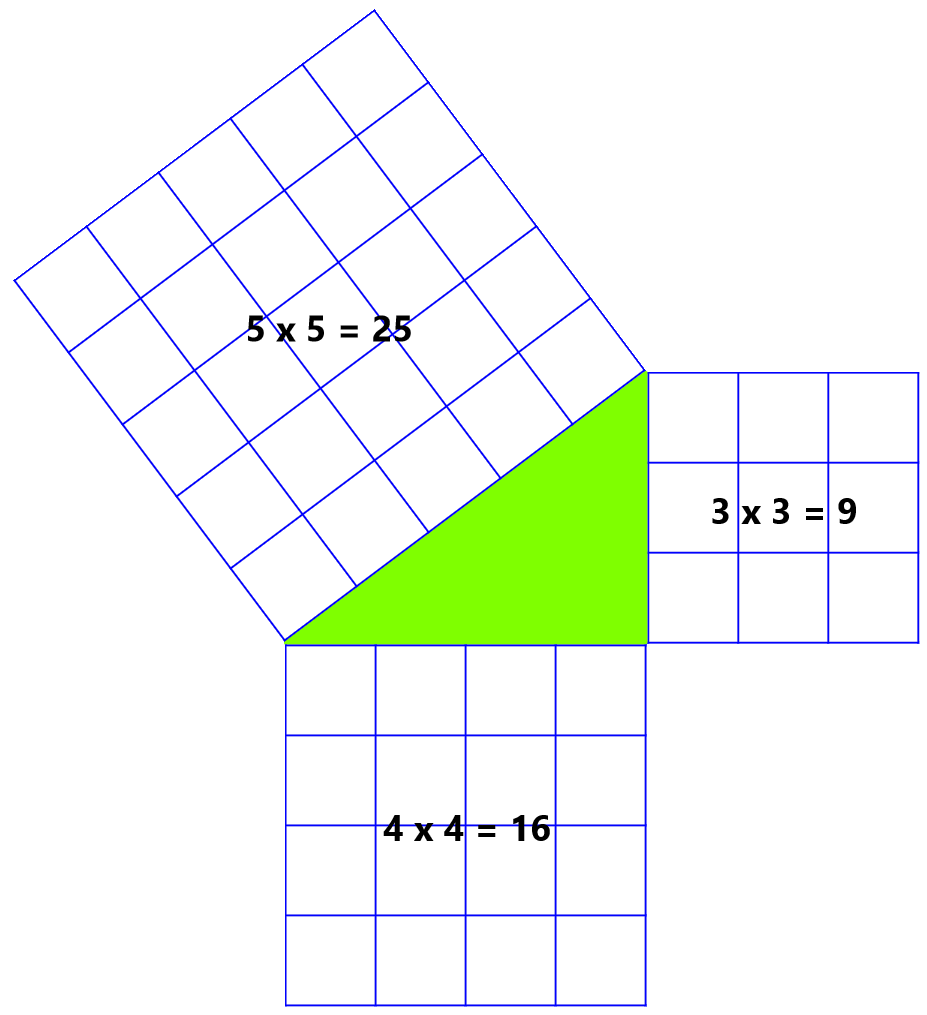
Máme pravoúhlý trojúhelník, kde první odvěsna měří 3 (jednotky) a druhá odvěsna se rovná 4. Pak přepona se rovná 5. Vycházíme tedy z rovnice:
\(5^2=3^2+4^2\) ... když umocníme jednotlivé hodnoty délek stran, vychází nám \(25=9+16\)

Matematika je krásná

Zajímavost: Podívej se na krásu matematiky. Říká se ji Fraktální Pythagorův strom